An international team of German, Austrian, and American researchers led by Barna Páll-Gergely (HUN-REN Centre for Agricultural Research, Plant Protection Institute) and András A. Sipos (HUN-REN-BME Morphodynamics Research Group) investigated the structure and economics of shells of different land snail species. According to their findings, published in the prestigious journal Evolution, while a globular shell door limits the variation in the shape of the aperture for the door snails, there is no such limit for the stylommatophoran snails, so evolution has more freedom to optimise the shape of their shells. This difference may have played a role in the evolutionary success of stylommatophoran snails over door snails.
Two groups make up the majority of the nearly 30,000 known land molluscs (snails and slugs). The larger group is known as the air-breathing molluscs (Stylommatophora), with almost 23,000 species distributed almost everywhere on Earth. The vast majority of species living in Hungary belong to this group. The smaller group is Cyclophoroidea, with nearly 4,000 species, mainly referring to snails distributed in the tropics. The latter have a door called the operculum (which closes the entrance to the snail shell when the snail retreats into it), so they can also be called door snails.
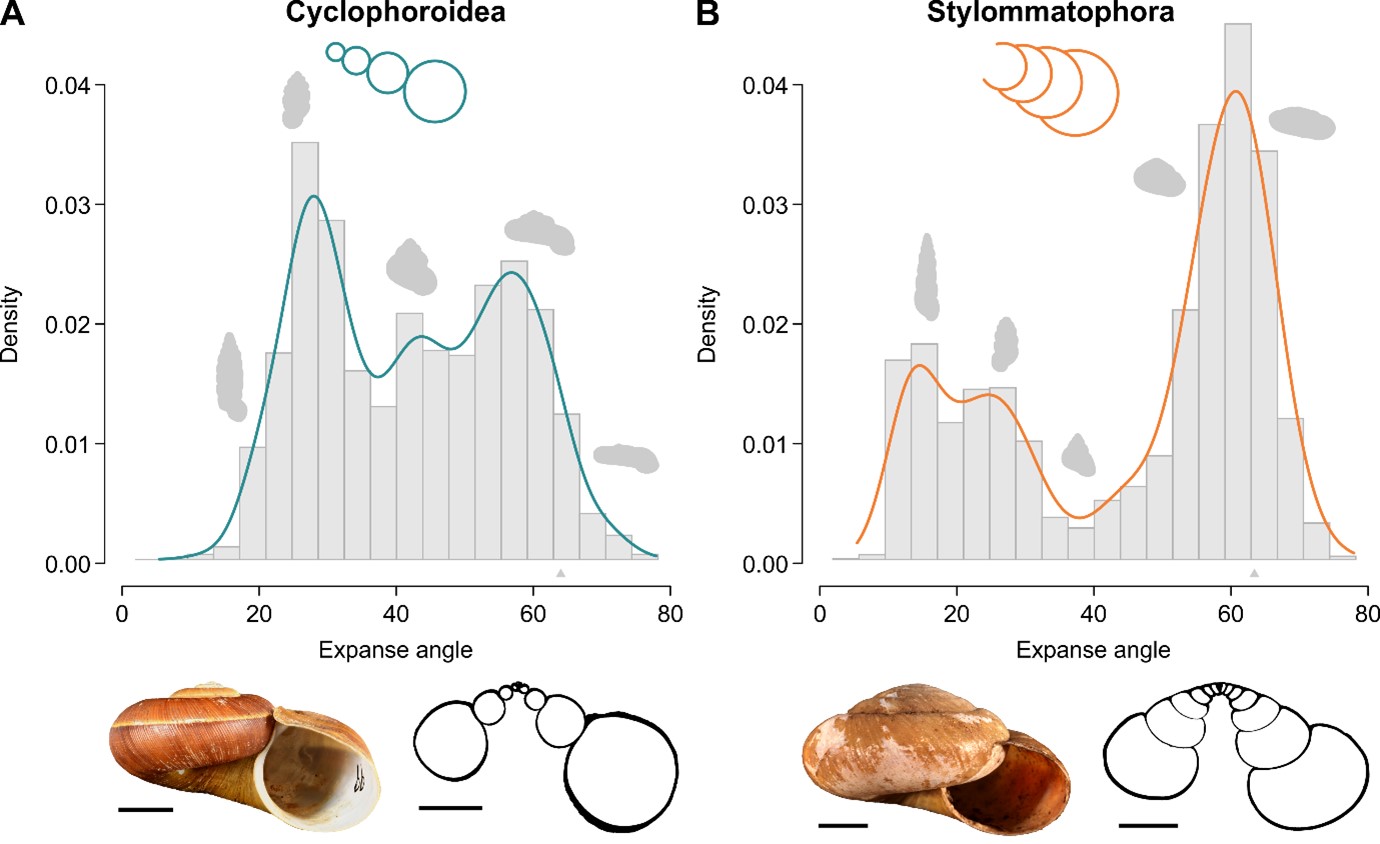
The figure below summarises the differences between the shells of the two groups. The diagrams show, from left to right, the frequency of progressively flatter shells observed in nature. As the door of the door snails (A: bottom left photo and CT cross-section) is primarily round, the entrance to the snail shell is also similar in shape. This implies that the cross-sections of the bends are also round and that successive bends only touch at a single point.
In contrast, the shape of the entrance to the stylommatophoran snails (B: bottom right photo and CT section) is more varied, usually crescent-shaped, as the subsequent bends may be more closely superimposed on the preceding ones. Furthermore, it has been known since the 1970s that flat and tall coiled shells are abundant among stylommatophoran snails, but globular shapes (i.e., shell height and shell width are roughly equal) are very rare (right diagram).
Maxima associated with flat and tall shells are also observed among door snails (left diagram), but species with shells roughly equal in width and height are much more common than in stylommatophoran snails.
The difference in shell frequency between the two groups has not been explained by measurements so far. Hence, German, Austrian and American researchers led by Barna Páll-Gergely and Árpád András Sipos examined CT scans of the shells of 39 gastropod species and analytically studied the shell geometry.
The study's hypothesis states that the observed difference in frequency is related to the optimal, i.e., material-efficient, shell shape. In principle, snails strive for minimum material consumption, which means they try to enclose a given volume with a shell of minimum surface area. In applied mathematics, the efficiency of a geometric shape, in this sense, is characterised by the so-called isoperimetric ratio. In the case of a gastropod shell, the isoperimetric ratio can be defined both for the typical curved cross-section and the total three-dimensional surface.
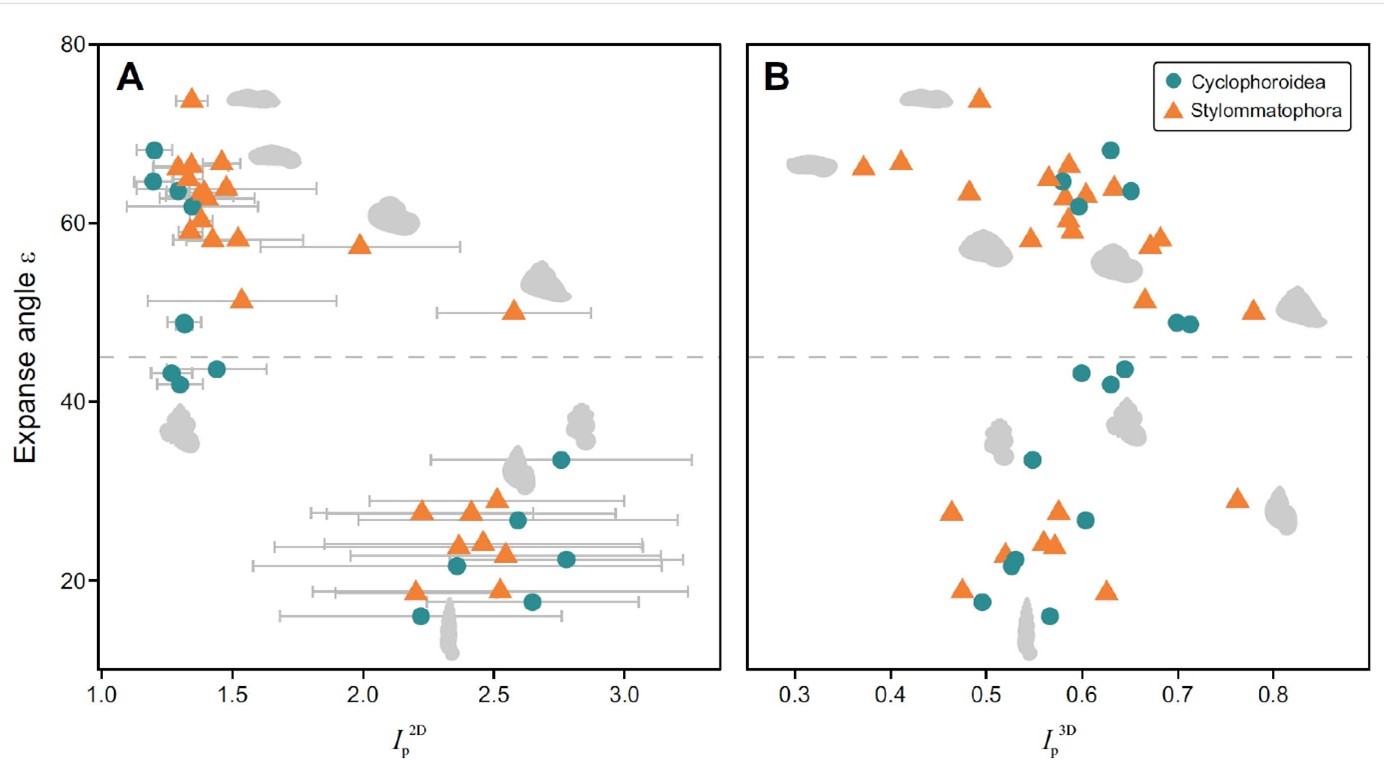
The tests performed in two dimensions (left figure) showed that the cross-sectional isoperimetric ratio of the lung snails is higher since the successive bends overlap substantially, while in the case of the door snails, more material is needed to construct the touching circular cross-sections. It can be theoretically demonstrated that there exists an optimal degree of overlap of successive bends where the isoperimetric ratio attains a maximum. The results of measurements based on CT scans cluster around this optimum. However, the door coils cleverly compensate for the disadvantage of the circular cross-section: the efficiency of the shape is ensured by the three-dimensional arrangement of the form (right figure) by building shells with higher spires and narrower umbilicus. This, however, means that there will be proportionally more globular shells in the door snail group, explaining the discrepancy seen in the frequency diagrams.
For high-coiled (tower-like) shells, there is no significant difference between the isoperimetric ratios of the two groups. This is explained by the fact that a given bend meets the previous bend at two points rather than one, which further reduces the amount of material needed to make the shell to the extent that the actual shape of the cross-section does not significantly affect the isoperimetric ratio.
In summary, while the presence of a globular shell door limits the variation in the shape of the aperture for the door snails, there is no such limit for the stylommatophoran snails, so evolution has more freedom to optimise the shape of their shells. This difference may partly explain the different species numbers and evolutionary success of the two groups.